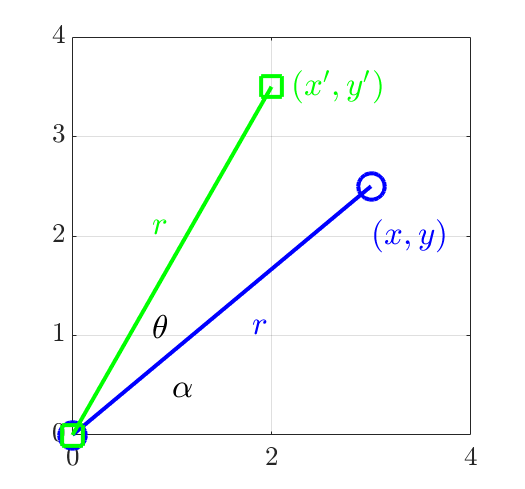
Derivation of 2D Rotation Matrix
The rotation matrix is pretty well known in mechanics
\[R = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix}\]In order to derive it, we first know that
\[\begin{cases} x = r \cos(\alpha) \\ y = r \cos(\alpha) \\ x' = r \cos(\alpha+\theta) \\ y' = r \cos(\alpha+ \theta) \end{cases}\]By using trigonometric identities, we are able to reduce $x’$ and $y’$
\[\begin{align} x' &= r \cos(\alpha + \theta) \\ &= r [\cos(\alpha)\cos(\theta) - \sin(\alpha)\sin(\theta)] \\ &= r \cos(\alpha)\cos(\theta) - r \sin(\alpha)\sin(\theta) \\ &= x\cos(\theta) - y\sin(\theta) \\ \end{align}\] \[\begin{align} y' &= r \sin(\alpha + \theta) \\ &= r [\sin(\alpha)\cos(\theta) - \cos(\alpha)\sin(\theta)] \\ &= r \sin(\alpha)\cos(\theta) - r \cos(\alpha)\sin(\theta) \\ &= y\cos(\theta) - x \sin(\theta) \\ \end{align}\]Therefore, we are able to say that \(\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} x \\ y \end{bmatrix} \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix}\)
The rotation matrix is really just a matrix that may assume the form of a transformation matrix if one multiplies a 2D cartesian vector by it
3D Rotation Matrices
Just for fun, here are the rotation matrices for three dimesions. The subscript indicates the axis in which the rotation matrix is about. For example, \(R_x\) is the rotation matrix about the \(x\) axis.
\[R_x = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) \\ 0 & \sin(\theta) & \cos(\theta) \end{bmatrix}\] \[R_y = \begin{bmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{bmatrix}\] \[R_z = \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0\\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}\]