So the gradient descent is one of the best starting points that I can think of when trying to get into machine learning.
Theory
Calculus
In calculus, one of the first things that one learns is to attain the minimum and/or maximum of a function. Usually, the method of choice is to take the first derivative and then set it to zero, and solve for the input argument (e.g. \(x\))
As an example, let’s find the minimum of the function \(y(x)\)
\[\begin{align*} y(x) &= x^2 + 4x - 10 \quad (\text{Take the derivative}) \\ \frac{dy(x)}{dx} &= \frac{d}{dx} \left[ x^2 + 4x - 10 \right] \\ &= 2x + 4 \quad (\text{Set the derivative equal to zero}) \\ 0 &= 2x + 4 \\ -2x &= 4 \\ x &= -2 \end{align*}\]Therefore in this case, the minimum occurs at \(x = -2\)!
If this was a gradient descent problem, the final theoretical solution would be \(x \approx -2\), and instead of \(x\) would be the weights \(w\)
Back to Gradient Descent
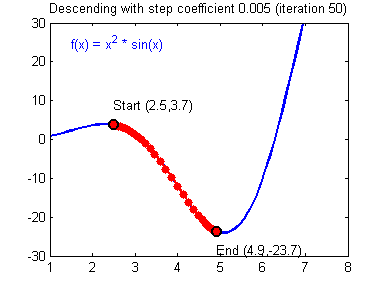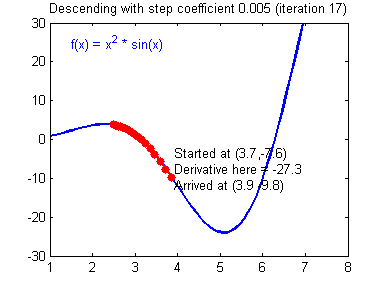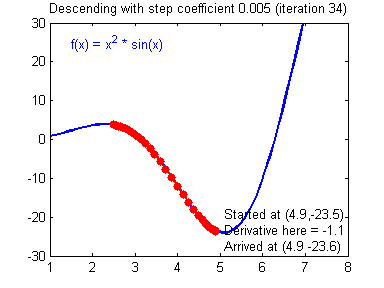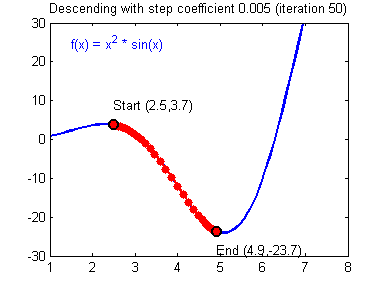
So that was easy! Gradient descent follows on that same concept. HOWEVER, although it tries to find the minimum, it does not know the function equivalent to \(y(x)\). However, since it uses the gradient \(\nabla\), it uses it to walk down the hill.
So, in this case, we define:
| Variables | |
|---|---|
| \(x = \text{Features}\) | \(m = \text{Slope}\) |
| \(y = \text{Label}\) | \(w = [m,b] = \text{weights}\) |
| \(b = \text{Bias}\) | \(n = \text{Number of Observations}\) |
In this case, you will likely have \(n\) observations, and you will have a model. The model is simply a model and it is not optimized for your data. Your goal in such case is to discover the weights \(w\), such that they fit your data.
Define Model
For a linear model,
\[y_{pred,i} = mx_i + b\]Define Residual or Error
The residual of the prediction would be
\[\text{Residual} = \text{Truth} - \text{Prediction}\] \[\text{Residual} = y_{true,i} - y_{pred,i}\] \[\text{Residual} = y_{true,i} - (mx_i + b)\]Define Cost
For the cost function, we can use the Mean Squared Error
\[MSE = \frac{1}{N} \sum_{i=1}^n \text{Residual}^2\] \[MSE = \frac{1}{N} \sum_{i=1}^n \left[ y_{true,i} - (mx_i + b) \right]^2\]You can consider your cost energy function as \(MSE\), and with that you can also compute its gradient \(\nabla MSE\)
Evolve Weights
All you have to do now is to define an initial set of weights. Do you know them? Nope! So you can choose any and then you can try different initial weights \(w_0\) for different experiments. You have to also define a learning rate \(\gamma\). So with that, now you should have:
- Cost function \(MSE\)
- Gradient of Cost Function \(\nabla MSE\)
- Initial Weights \(w_0\)
- Learning Rate \(\gamma\)
Now to evolve the weights,
Initialize weights \(w\)
for each step:
Make label predictions using \(w\)
Determine Cost (Optional)
Determine Gradient of Cost \(\nabla MSE\)
Update weights: \(w_{new} = w_{old} - \gamma \nabla MSE\)
After many iterations, the weights will be minimized! Let’s take a look at some examples!
Application: Simple Regression Example
Let’s import the libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
Problem
Let’s say you are given a set of data \(\textbf{x}\), where \(\textbf{x} \in \mathbb{R}^{1 \times n}\). Let’s say \(x\) is the number of bananas. Along with that, it comes with labels \(y\), which indicate the number of monkeys that come to your house! We are given a plot like the one below
[INSERT SCATTER PLOT]
We are trying to setup a linear regression to the data so that you can start to make predictions. We can set the model to be a linear model
\[y = m\textbf{x} + b\]which in turn can be reduced to
\[y = \textbf{w} \cdot \textbf{x}\]Where we can redefine \(\textbf{x} \in \mathbb{R}^{2\times n}\), where all of the elements of the second row are \(1\)s. This way, we can say that \(\textbf{w} \in \mathbb{R}^{2 \times 1}\), creating the model
Let’s Get Started!
def Model(w,x):
y_pred = np.matmul(w.T, x).T
return y_pred
Our cost function is defined as
\[MSE = \frac{1}{N} \sum_{i=1}^n \left[ y_{true,i} - (mx_i + b) \right]^2\]def cost_function(w,x,y):
N = len(x)
m = w[0]
b = w[1]
totalError = 0.0
for k in range(N):
totalError = totalError + (y - (np.dot(m,x) + b))**2
return totalError/N
In order to calculate the gradient, we know that our MSE for our model is dependent on $m$ and $b$, \(MSE(m,b) = \frac{1}{N} \sum_{i=1}^n (y_i - (mx_i + b))^2\)
Therefore, the gradient is: \(\nabla MSE = \begin{bmatrix} \frac{\partial MSE}{\partial m} \\ \frac{\partial MSE}{\partial b} \end{bmatrix} = \begin{bmatrix} \frac{1}{N} \sum (-2x_i)(y_i - (mx_i + b)) \\ \frac{1}{N} \sum (-2)(y_i - (mx_i + b)) \\ \end{bmatrix}\)
def gradient_function(w,x,y):
N = len(x)
m = w[0]; b = w[1]
dMSE_dm = 0
dMSE_db = 0
for k in range(1): # For every feature
dMSE_dm = -2 * x[k] * ( y - (np.dot(m,x) + b));
dMSE_db = -2 * (y - (np.dot(m,x) + b))
dMSE_dm = dMSE_dm / float(N)
dMSE_db = dMSE_db / float(N)
return [dMSE_dm, dMSE_db]
We can then initialize the guess and the learning rate \(\gamma\)
w = np.array([[1],[1]])
learningRate = 0.05
You can then run the main algorithm
def mainAlgorithm():
global w
global learningRate
global printResults
cost_array = [];
label_array = [];
numSteps = 10000
for k in range(numSteps):
cost = cost_function(w,x,y)
grad = gradient_function(w,x,y)
# Append items to arrays
cost_array.append(cost)
label_array.append(label_ser[k])
# Update Weights
w = w - grad*learningRate
[INSERT FIGURES]
Application: Multi-Dimensional Example
If you are to have a dataset with multiple features \(f\), we can say that \(x \in \mathbb{R}^{f \times n}\), all we have to do is to make a more modular setup.
Let’s import some libraries!
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import scipy.io as spio
import sys
# For plotting in 3D
from mpl_toolkits.mplot3d import Axes3D
We can create a class LinearRegression_Tool
class LinearRegression_Tool:
# PARTIAL
For this class, we can create the initializer, such that it also takes care of the dimensions, making sure that all of the linear algebra will work out super nicely later on!
# PARTIAL
def __init__(self,features,labels):
self.lr = 0.00005
try:
features.shape[1]
arrayOnes = np.ones((features.shape[0],1))
self.feats = np.append(features, arrayOnes, axis=1)
self.feats = self.feats.T
except:
arrayOnes = np.ones((features.shape[0],1));
features = np.reshape(features,(len(features),1));
self.feats = np.append(features, arrayOnes, axis=1)
self.feats = self.feats.T
try:
labels.shape[1]
self.y_true = labels
except:
labels = np.reshape(labels,(len(labels),1))
self.y_true = labels
We can create some Setters and Getters
# PARTIAL
def setWeights(self,weights):
if type(weights) is not np.ndarray:
print('This is not a numpy array')
sys.exit(0)
elif weights.shape[1] != 1:
print('This is not a column vector')
elif weights.shape[0] != self.feats.shape[0]:
print('The number of weights do not coincide with the number of features')
else:
self.w = weights
self.init_w = weights
#---------------------------------------------------------------------------
def getWeights(self):
return self.w
#---------------------------------------------------------------------------
def setLearningRate(self,lr):
self.lr = lr
#---------------------------------------------------------------------------
def getErrorArray(self):
return self.errorArray
We create the model, in this case a linear model
# PARTIAL
def Model(self):
y_pred = np.matmul(self.w.T,self.feats).T
return y_pred
We can create the cost function
# PARTIAL
def SquaredLoss(self):
self.y_pred = self.Model()
error = (self.y_true - self.y_pred)**2
totalError = np.sum(error)/error.size
print('Total Error is %.2f' % totalError)
return totalError
We can create the gradient of the cost function
# PARTIAL
def GradientSquaredLoss(self):
GradE = -2*self.w*np.sum(self.y_true - self.Model())/self.y_true.size
return GradE
We then create a weights updater
# PARTIAL
def UpdateWeights(self):
self.w = self.w - self.lr*self.GradientSquaredLoss()
Finally, we setup a evolution function
# PARTIAL
def Evolve_threshold(self,threshold=0.0001,num_iterations = 1000, showEvolution=False):
self.errorArray = np.ones((num_iterations,1))
for k in range(num_iterations):
self.UpdateWeights()
thisError = self.SquaredLoss()
self.errorArray[k] = thisError
if showEvolution == True:
self.plotResults()
if np.abs(thisError-self.errorArray[k-1]) < threshold:
n = 1000-k
self.errorArray = self.errorArray[:-n]
break
Final Code
The final code will look like the following
class LinearRegression_Tool:
#---------------------------------------------------------------------------
def __init__(self,features,labels):
self.lr = 0.00005
try:
features.shape[1]
arrayOnes = np.ones((features.shape[0],1))
self.feats = np.append(features, arrayOnes, axis=1)
self.feats = self.feats.T
except:
arrayOnes = np.ones((features.shape[0],1));
features = np.reshape(features,(len(features),1));
self.feats = np.append(features, arrayOnes, axis=1)
self.feats = self.feats.T
try:
labels.shape[1]
self.y_true = labels
except:
labels = np.reshape(labels,(len(labels),1))
self.y_true = labels
#---------------------------------------------------------------------------
def setWeights(self,weights):
if type(weights) is not np.ndarray:
print('This is not a numpy array')
sys.exit(0)
elif weights.shape[1] != 1:
print('This is not a column vector')
elif weights.shape[0] != self.feats.shape[0]:
print('The number of weights do not coincide with the number of features')
else:
self.w = weights
self.init_w = weights
#---------------------------------------------------------------------------
def getWeights(self):
return self.w
#---------------------------------------------------------------------------
def setLearningRate(self,lr):
self.lr = lr
#---------------------------------------------------------------------------
def Model(self):
y_pred = np.matmul(self.w.T,self.feats).T
return y_pred
#---------------------------------------------------------------------------
def SquaredLoss(self):
self.y_pred = self.Model()
error = (self.y_true - self.y_pred)**2
totalError = np.sum(error)/error.size
print('Total Error is %.2f' % totalError)
return totalError
#---------------------------------------------------------------------------
def GradientSquaredLoss(self):
GradE = -2*self.w*np.sum(self.y_true - self.Model())/self.y_true.size
return GradE
#---------------------------------------------------------------------------
def UpdateWeights(self):
self.w = self.w - self.lr*self.GradientSquaredLoss()
#---------------------------------------------------------------------------
def Evolve_threshold(self,threshold=0.0001,num_iterations = 1000, showEvolution=False):
self.errorArray = np.ones((num_iterations,1))
for k in range(num_iterations):
self.UpdateWeights()
thisError = self.SquaredLoss()
self.errorArray[k] = thisError
if showEvolution == True:
self.plotResults()
if np.abs(thisError-self.errorArray[k-1]) < threshold:
n = 1000-k
self.errorArray = self.errorArray[:-n]
break
#---------------------------------------------------------------------------
def getErrorArray(self):
return self.errorArray
#---------------------------------------------------------------------------
def plotResults(self):
if self.w.shape[0] == 2:
# This is a 2D plot
plt.figure()
plt.plot(self.feats[0,:],self.y_true,'bo-',label="True Data")
plt.plot(self.feats[0,:],self.Model(),'rx--',label='Predictions')
plt.plot(self.feats[0,:],np.matmul(self.init_w.T,self.feats).T,'g.--',label='Initial')
plt.legend()
plt.xlabel('Input Data')
elif self.w.shape[0] == 3:
# This is a 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# FINISH THIS
else:
print('This data cannot be displayed in a graph. It has dimensions higher than possible')
Usage
# Load a .mat file
ls_lm = spio.loadmat('./ls_lm.mat',squeeze_me=True)
x = ls_lm['x']
y = ls_lm['y']
# Create the class as a tool
LinReg = LinearRegression_Tool(x,y)
# Perform the actions
weights = np.array([[2],[5]])
LinReg.setWeights(weights)
LinReg.Evolve_threshold()
errors = LinReg.getErrorArray()
# Get the final weights
finalWeights = LinReg.getWeights()
# Plot the results
plt.plot(errors)
LinReg.plotResults()
plt.show()